Dosen: Pak Hermanto, M. Kom
Materi Aljabar Linier dan Matriks Lengkap
Assalammualaikum wr. wb., Salam sejahtera untuk kita semua semoga apa yang dibaca dan dipelajari dapat membuahkan suatu hasil yang nantinya akan berguna untuk bangsa, amin. Materi ini saya dapatkan dari dosen Aljabar Linier yaitu Ibu Mia Mayang Sari, S.Kom. Dalam artikel ini ada beberapa silabus yang akan dibahas dalam ruang lingkup aljabar linier dan matriks, diantaranya adalah sebagai berikut :
- Aljabar Linier Dalam Bidang Informatika
- Basis dan Ruang Vektor
- Matriks dan Determinan
- Sistem Persamaan Linear
- Konsep Nilai Eigen dan Vektor Eigen
- Matlab
Assalammualaikum wr. wb., Salam sejahtera untuk kita semua semoga apa yang dibaca dan dipelajari dapat membuahkan suatu hasil yang nantinya akan berguna untuk bangsa, amin. Materi ini saya dapatkan dari dosen Aljabar Linier yaitu Ibu Mia Mayang Sari, S.Kom. Dalam artikel ini ada beberapa silabus yang akan dibahas dalam ruang lingkup aljabar linier dan matriks, diantaranya adalah sebagai berikut :
- Aljabar Linier Dalam Bidang Informatika
- Basis dan Ruang Vektor
- Matriks dan Determinan
- Sistem Persamaan Linear
- Konsep Nilai Eigen dan Vektor Eigen
- Matlab
ALJABAR LINIER DAN MATRIKS DALAM BIDANG INFORMATIKA
Definisi / Pegnertian Aljabar Linier dan Matriks
- Aljabar linier adalah bidang studi yang mempelajari sistem persamaan linier dan solusinya, vektor serta transformasi linier.
- Matriks adalah kumpulan bilangan, simbol atau ekspresi berbentuk persegi panjang yang disusun menurut baris dan kolom.
- Aljabar linier dan matriks merupakan bagian yang sangat berkaitan, matriks merupakan operasi dalam pencarian persamaan aljabar linier.
Contoh Persamaan Linier :
x + y = 4 (persamaan linier dengan 2 peubah)
2x-3y=2z+1 (persamaan linier dengan 3 peubah)
- Aljabar linier adalah bidang studi yang mempelajari sistem persamaan linier dan solusinya, vektor serta transformasi linier.
- Matriks adalah kumpulan bilangan, simbol atau ekspresi berbentuk persegi panjang yang disusun menurut baris dan kolom.
- Aljabar linier dan matriks merupakan bagian yang sangat berkaitan, matriks merupakan operasi dalam pencarian persamaan aljabar linier.
Contoh Persamaan Linier :
x + y = 4 (persamaan linier dengan 2 peubah)
2x-3y=2z+1 (persamaan linier dengan 3 peubah)
Aljabar Linier dalam Bidang Informatika
- Kriptografi : penggunaan teknik matriks identitas
- Komputer Grafik : penggunaan teknik matriks transpose
- Games : penggunaan berbagai macam teknik matriks
- Pengolahan Citra : penggunaan teknik matriks dan persamaan linier
- Kriptografi : penggunaan teknik matriks identitas
- Komputer Grafik : penggunaan teknik matriks transpose
- Games : penggunaan berbagai macam teknik matriks
- Pengolahan Citra : penggunaan teknik matriks dan persamaan linier
BASIS RUANG DAN VEKTOR
Definisi / Pengertian Basis
- Basis adalah himpunan vektor.
- Basis juga bisa dianggap sebagai sistem koordinat.
- Misalkan V ruang vektor dan S = { s 1, s 2 ,…, s n }. S disebut basis dari V.
- Basis adalah himpunan vektor.
- Basis juga bisa dianggap sebagai sistem koordinat.
- Misalkan V ruang vektor dan S = { s 1, s 2 ,…, s n }. S disebut basis dari V.
Vektor Basis di Ruang R2
Vektor basis diruang R2 pada sumbu X dinyatakan dengan i, vektor satuan pada sumbu Y dinyatakan dengan j
Bentuk vektor baris ditulis sebagai berikut : e1 = (1,0), e2 = (0,1)
Vektor basis diruang R2 pada sumbu X dinyatakan dengan i, vektor satuan pada sumbu Y dinyatakan dengan j
Bentuk vektor baris ditulis sebagai berikut : e1 = (1,0), e2 = (0,1)
Vektor Basis di Ruang R3
Vektor basis diruang R3 pada sumbu X dinyatakan dengan i, pada sumbu Y dinyatakan dengan j, sedangkan vektor satuan pada sumbu Z dinyatakan dengan k.
Bentuk vektor baris ditulis sebagai berikut : e1 = (1,0,0), e2 = (0,1,0), e3 = (0,0,1)
Vektor basis diruang R3 pada sumbu X dinyatakan dengan i, pada sumbu Y dinyatakan dengan j, sedangkan vektor satuan pada sumbu Z dinyatakan dengan k.
Bentuk vektor baris ditulis sebagai berikut : e1 = (1,0,0), e2 = (0,1,0), e3 = (0,0,1)
Vektor di Ruang R2
- Vektor terletak sepanjang sumbu koordinat X dan Y.
- Vektor berada di R2 maka dikatakan vektor berada di bidang.
- Vektor terletak sepanjang sumbu koordinat X dan Y.
- Vektor berada di R2 maka dikatakan vektor berada di bidang.
Vektor di Ruang R3
- Vektor dalam ruang digambarkan dalam sistem koordinat ruang.
- Sumbu X dan Y mendatar sedangkan sumbu Z vertikal.
- Ketiga sumbu tersebut saling tegak lurus dan perpotongan dititik pangkal O (0,0,0).
- Vektor dalam ruang digambarkan dalam sistem koordinat ruang.
- Sumbu X dan Y mendatar sedangkan sumbu Z vertikal.
- Ketiga sumbu tersebut saling tegak lurus dan perpotongan dititik pangkal O (0,0,0).
Pengantar Vektor
- Didalam Fisika dikenal 2 buah besaran, yaitu besaran skalar dan besaran vektor.
- Skalar adalah besaran yang hanya memiliki nilai.
- Contoh skalar : massa.
- Vektor didefinisikan sebagai sebuah besaran yang memiliki nilai dan arah.
- Contoh vektor : Kecepatan.
- Didalam Fisika dikenal 2 buah besaran, yaitu besaran skalar dan besaran vektor.
- Skalar adalah besaran yang hanya memiliki nilai.
- Contoh skalar : massa.
- Vektor didefinisikan sebagai sebuah besaran yang memiliki nilai dan arah.
- Contoh vektor : Kecepatan.
Notasi Vektor
- Vektor merupakan garis berarah yang memiliki titik awal dan titik akhir.
- Arah panah menunjukan arah vektor dan panjang vektor menunjukan besaran vektor.
- Vektor dapat ditulis dengan huruf kecil tebal atau tanda bar.
- Vektor merupakan garis berarah yang memiliki titik awal dan titik akhir.
- Arah panah menunjukan arah vektor dan panjang vektor menunjukan besaran vektor.
- Vektor dapat ditulis dengan huruf kecil tebal atau tanda bar.
Gambar Vektor
Gambar Vektor
- Titik pangkal di A
- Titik ujung di B
- Arah vektor di A menuju B
- Besar vektor ditunjukan oleh panjang garis AB
 |
| Gambar Vektor |
- Titik pangkal di A
- Titik ujung di B
- Arah vektor di A menuju B
- Besar vektor ditunjukan oleh panjang garis AB
Operasi-operasi Pada Vektor
- Kesamaan dua vektor
- Negatif sebuah vektor
- Resultan 2 buah vektor
- Penjumlahan vektor
- Perkalian vektor dengan skalar
- Kesamaan dua vektor
- Negatif sebuah vektor
- Resultan 2 buah vektor
- Penjumlahan vektor
- Perkalian vektor dengan skalar
Kesamaan Dua Vektor
Suatu vektor dikatakan sama apabila memiliki panjang dan arah yang sama, dengan tidak memperhatikan titik pangkal.
Gambar Kesamaan Dua Vektor
Suatu vektor dikatakan sama apabila memiliki panjang dan arah yang sama, dengan tidak memperhatikan titik pangkal.
 |
| Gambar Kesamaan Dua Vektor |
Negatif Sebuah Vektor
Vektor (-a) adalah vektor yang memiliki arah berlawanan dengan vektor a tetapi panjangnya sama dengan vektor a.
Gambar Negatif Sebuah Vektor
Vektor (-a) adalah vektor yang memiliki arah berlawanan dengan vektor a tetapi panjangnya sama dengan vektor a.
 |
| Gambar Negatif Sebuah Vektor |
Resultan 2 Buah Vektor
Resultan dua vektor u dan v adalah vektor w yang dibentuk dengan menempatkan titik pangkal vektor v pada titik ujung vektor v dan menghubungkan titik pangkal vektor u dengan titik ujung vektor v
Gambar Resultan 2 Buah Vektor
Resultan dua vektor u dan v adalah vektor w yang dibentuk dengan menempatkan titik pangkal vektor v pada titik ujung vektor v dan menghubungkan titik pangkal vektor u dengan titik ujung vektor v
|
| Gambar Resultan 2 Buah Vektor |
Penjumlahan Vektor
Diketahui a dan b vektor–vektor di ruang yang komponen – komponennya adalah
a = ( a1,a2,a3 ) dan b = ( b1,b2,b3 )
Maka :
a + b = (a1 +b1, a2+b2, a3+b3 )
Contoh :
diketahui dua vektor a = i+2j-3k dan b = 2i+5j+4k, berapakah a+b ?
Diketahui a dan b vektor–vektor di ruang yang komponen – komponennya adalah
a = ( a1,a2,a3 ) dan b = ( b1,b2,b3 )
Maka :
a + b = (a1 +b1, a2+b2, a3+b3 )
Contoh :
diketahui dua vektor a = i+2j-3k dan b = 2i+5j+4k, berapakah a+b ?
Perkalian Vektor dengan Skalar Aljabar Linier dan Matriks
Diketahui a vektor di ruang yang komponen – komponennya adalah a = ( a1,a2,a3 )
Maka k . a = ( ka1, ka2, ka3 )
Jika k > 0 maka searah dengan a
Jika k < 0 maka berlawanan arah dengan a
Contoh :
diketahui vektor a = i+2j-3k, maka 2a = ?
Diketahui a vektor di ruang yang komponen – komponennya adalah a = ( a1,a2,a3 )
Maka k . a = ( ka1, ka2, ka3 )
Jika k > 0 maka searah dengan a
Jika k < 0 maka berlawanan arah dengan a
Contoh :
diketahui vektor a = i+2j-3k, maka 2a = ?
Panjang Vektor
Panjang sebuah vektor u disebut juga norma u dinyatakan dengan :
Contoh : hitunglah panjang vektor u = 3i+4j!
Panjang sebuah vektor u disebut juga norma u dinyatakan dengan :
Contoh : hitunglah panjang vektor u = 3i+4j!
Jarak Euclidean Antara Dua Vektor
Jika p = (p1, p2,….pn) dan q = (q1, q2,…qn)
Contoh : diketahui p = (2i+3j) dan q = (5i + 6j), berapa jarak Euclideannya?
Jika p = (p1, p2,….pn) dan q = (q1, q2,…qn)
Contoh : diketahui p = (2i+3j) dan q = (5i + 6j), berapa jarak Euclideannya?
Contoh Penerapan Vektor dalam Klasifikasi Citra
Diketahui tiga buah wajah, yaitu Citra 1(Dilla), Citra 2 (Agil), dan Citra 3 (Alim)yang akan digunakan sebagai basis data untuk pengenalan pola wajah menggunakan komputer.
Beberap ciri untuk mengenali citra tersebut adalah dilihat dari standar deviasi intensitas warna dalam tiap-tiap citra σ, rata-ratanya µ, dan entropinya ℯ. Setelah ketiga ciri tersebut dihitung diperoleh data berikut:
Citra 1: σ=0,15 µ=40 ℯ=1,25
Citra 2: σ=0,05 µ=60 ℯ=2,35
Citra 3: σ=0,24 µ=53 ℯ=0,85
Kemudian diambil satu citra lagi, yaitu citra ke-4 sebagai citra uji.
Pada citra uji dihitung nilai-nilai ciri citra tersebut,diperoleh data berikut:
Citra 4: σ=0,23 µ=55 ℯ=0,82
Tentukan bagaimana komputer bisa mengenali citra ke-4?Dan siapakah nama dari citra ke-4 menurut hasil pengenalan komputer?
Diketahui tiga buah wajah, yaitu Citra 1(Dilla), Citra 2 (Agil), dan Citra 3 (Alim)yang akan digunakan sebagai basis data untuk pengenalan pola wajah menggunakan komputer.
Beberap ciri untuk mengenali citra tersebut adalah dilihat dari standar deviasi intensitas warna dalam tiap-tiap citra σ, rata-ratanya µ, dan entropinya ℯ. Setelah ketiga ciri tersebut dihitung diperoleh data berikut:
Citra 1: σ=0,15 µ=40 ℯ=1,25
Citra 2: σ=0,05 µ=60 ℯ=2,35
Citra 3: σ=0,24 µ=53 ℯ=0,85
Kemudian diambil satu citra lagi, yaitu citra ke-4 sebagai citra uji.
Pada citra uji dihitung nilai-nilai ciri citra tersebut,diperoleh data berikut:
Citra 4: σ=0,23 µ=55 ℯ=0,82
Tentukan bagaimana komputer bisa mengenali citra ke-4?Dan siapakah nama dari citra ke-4 menurut hasil pengenalan komputer?
MATRIKS
Definisi / Pengertian Matriks
Matriks adalah sekumpulan bilangan yang disusun dalam sebuah empat persegi panjang, secara teratur, di dalam baris-baris dan kolom-kolom.
Gambar Matriks
Matriks di atas disebut matriks ukuran m x n
Matriks adalah sekumpulan bilangan yang disusun dalam sebuah empat persegi panjang, secara teratur, di dalam baris-baris dan kolom-kolom.
 |
| Gambar Matriks |
Matriks di atas disebut matriks ukuran m x n
Operasi-operasi pada Matriks
1. Kesamaan Dua Buah Matriks
Dua matriks A dan B disebut sama, jika ukurannya sama dan berlaku : [ aij ] = [ bij ]
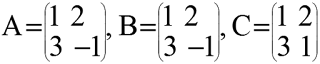A = B
A ≠ C
B ≠ C
2. Penjumlahan dua matriks
Jumlah dua buah matriks A + B bisa dilakukan asalkan kedua matriks tersebut berukuran sama
Sifat-sifat penjumlahan:
Komutatif : A + B = B + A
Assosiatif : A + (B + C) = (A + B) + C
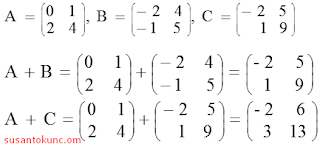3. Perkalian Matriks dengan Skalar
Jika k suatu skalar, maka matriks kA = (kaij)
Diperoleh dengan mengalikan semua elemen matriks A dengan k
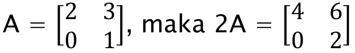4. Pengurangan Matriks
Mengurangi matriks A dengan B (A-B) adalah menjumlahkan matriks A dengan matriks (-B)
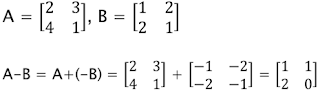5. Perkalian Matriks
Syarat perkalian matriks : banyaknya kolom matriks pertama = banyaknya baris matriks kedua.
Hasil perkalian antara matriks A = [aij] berordo mxp, dengan matriks B = [bij] berordo pxn, adalah matriks C = [Cij] berordo mxn.
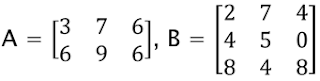
1. Kesamaan Dua Buah Matriks
Dua matriks A dan B disebut sama, jika ukurannya sama dan berlaku : [ aij ] = [ bij ]
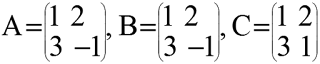
A = B
A ≠ C
B ≠ C
2. Penjumlahan dua matriks
Jumlah dua buah matriks A + B bisa dilakukan asalkan kedua matriks tersebut berukuran sama
Sifat-sifat penjumlahan:
Komutatif : A + B = B + A
Assosiatif : A + (B + C) = (A + B) + C
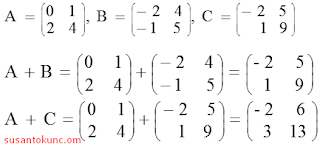
3. Perkalian Matriks dengan Skalar
Jika k suatu skalar, maka matriks kA = (kaij)
Diperoleh dengan mengalikan semua elemen matriks A dengan k
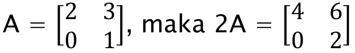
4. Pengurangan Matriks
Mengurangi matriks A dengan B (A-B) adalah menjumlahkan matriks A dengan matriks (-B)
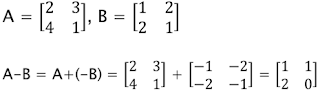
5. Perkalian Matriks
Syarat perkalian matriks : banyaknya kolom matriks pertama = banyaknya baris matriks kedua.
Hasil perkalian antara matriks A = [aij] berordo mxp, dengan matriks B = [bij] berordo pxn, adalah matriks C = [Cij] berordo mxn.
MACAM-MACAM MATRIKS
1. Matriks Bujursangkar Aljabar Linier dan Matriks
Matriks bujursangkar adalah matriks dimana banyaknya baris = banyaknya kolom
Gambar Matriks Bujur Sangkar
Matriks bujursangkar adalah matriks dimana banyaknya baris = banyaknya kolom
 |
| Gambar Matriks Bujur Sangkar |
2. Matrik Satuan / Identitas
- Matriks bujursangkar
- Setiap unsurnya nol, kecuali didiagonal utama = 1
Contoh :
Gambar Matrik satuan/ matriks identitas
- Matriks bujursangkar
- Setiap unsurnya nol, kecuali didiagonal utama = 1
Contoh :
 |
| Gambar Matrik satuan/ matriks identitas |
3. Matriks Segitiga
- Matriks bujursangkar
- Unsur di atas/di bawah diagonal utama adalah nol
Contoh :
Gambar Matriks Segitiga
- Matriks bujursangkar
- Unsur di atas/di bawah diagonal utama adalah nol
Contoh :
 |
| Gambar Matriks Segitiga |
4. Matriks Tranpose
- Tidak perlu bujursangkar
- Setiap baris ditukar tempat dengan kolom
- contoh :
Gambar Matriks Tranpose
- Tidak perlu bujursangkar
- Setiap baris ditukar tempat dengan kolom
- contoh :
Gambar Matriks Tranpose
5. Matriks Diagonal
- Matriks bujursangkar
- Semua unsur nol, kecuali didiagonal utama
Contoh :
Gambar Matriks Diagonal
- Matriks bujursangkar
- Semua unsur nol, kecuali didiagonal utama
Contoh :
 |
| Gambar Matriks Diagonal |
6. Aljabar Linier dan Matriks Nol
- Tidak perlu matriks bujur sangkar
- Semua unsurnya nol
Contoh :
Gambar Matriks Nol
- Tidak perlu matriks bujur sangkar
- Semua unsurnya nol
Contoh :
 |
| Gambar Matriks Nol |
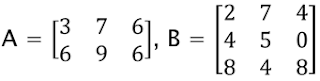
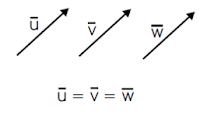
Tidak ada komentar:
Posting Komentar